Patterson Cylindrical Projection(帕特森圆柱投影)
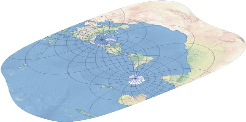
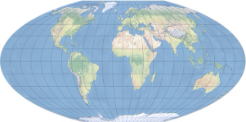
Patterson Cylindrical Projection(帕特森圆柱投影)是一种由汤姆·帕特森(Tom Patterson)于2014年设计的折衷型圆柱地图投影,旨在平衡大陆形状的可识别性与高纬度地区面积的过度夸大问题,其高宽比约为0.57,使地图呈现更紧凑的矩形外观;该投影的经线为等距平行直线,纬线也为直线且垂直于经线,但纬线间距在赤道至约60.5°纬度间逐渐增大,之后向两极收缩,从而在视觉上缓解极地变形;它既非等积也非等角,所有地理属性(形状、面积、距离、方向)在极区均有显著失真,但在中低纬度区域保持了较好的视觉一致性,因此常用于通用世界地图,尤其适合展示随经度变化的现象,如时区分布。
2026/02/09Natural Earth Projection(自然地球投影)
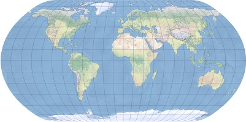
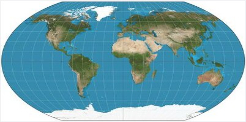
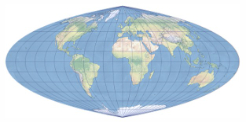
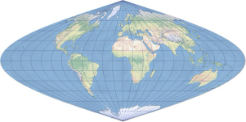
Natural Earth Projection(自然地球投影)是一种由Tom Patterson于2007年设计的折衷伪圆柱地图投影,专为全球世界地图的视觉呈现而优化。它不保持等角、也不保证等积,而是通过平滑的圆角过渡——横向经线与极线相交形成柔和曲线——来模拟地球的球形外观,从而在形状、面积与距离的综合失真之间取得优异平衡。该投影的变形模式对称于赤道和中央经线,高纬度地区面积略有夸大,角畸变在中心区域较轻,向边缘逐渐增强,整体视觉效果比Winkel Tripel或Robinson投影更自然、更贴近真实地球的视觉感受。
2026/02/06Kavrayskiy VII Projection(卡夫拉斯基第七投影)
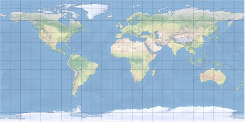
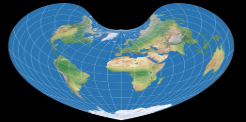
Kavrayskiy VII Projection(卡夫拉斯基第七投影)是一种伪圆柱形地图投影,由苏联地理学家 Vladimir V. Kavrayskiy 于1939年提出,旨在提供一种在视觉和数学上都较为均衡的世界地图表示方式。它通过将地球表面投影到一个二维平面,尽量平衡面积、形状、距离和方向的变形,整体畸变控制优于许多常用投影。该投影在赤道附近和中纬度区域的形变较小,尤其在45°范围内的形状保持较好,适合用于世界地图的通用展示。其数学表达简洁,常被用于GIS系统和数据可视化工具中,如R语言的googleVis包和Python的basemap库均支持该投影。
2026/02/05
 咨询客服
咨询客服